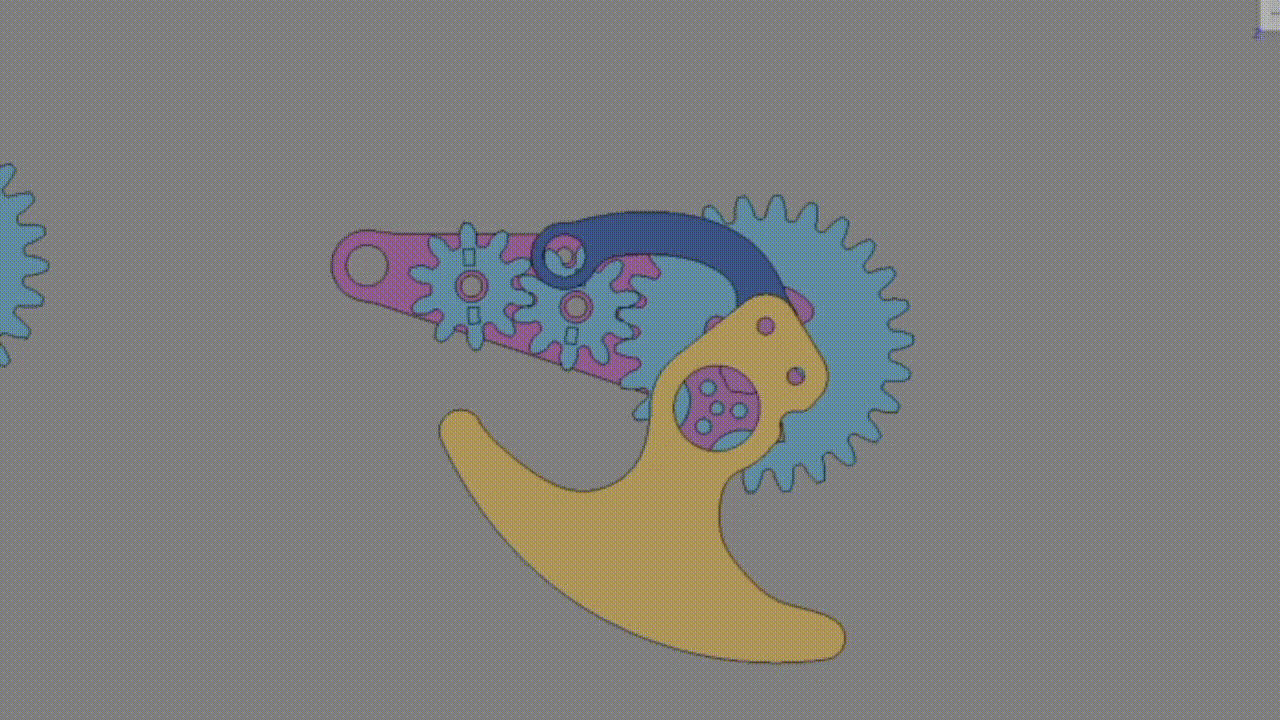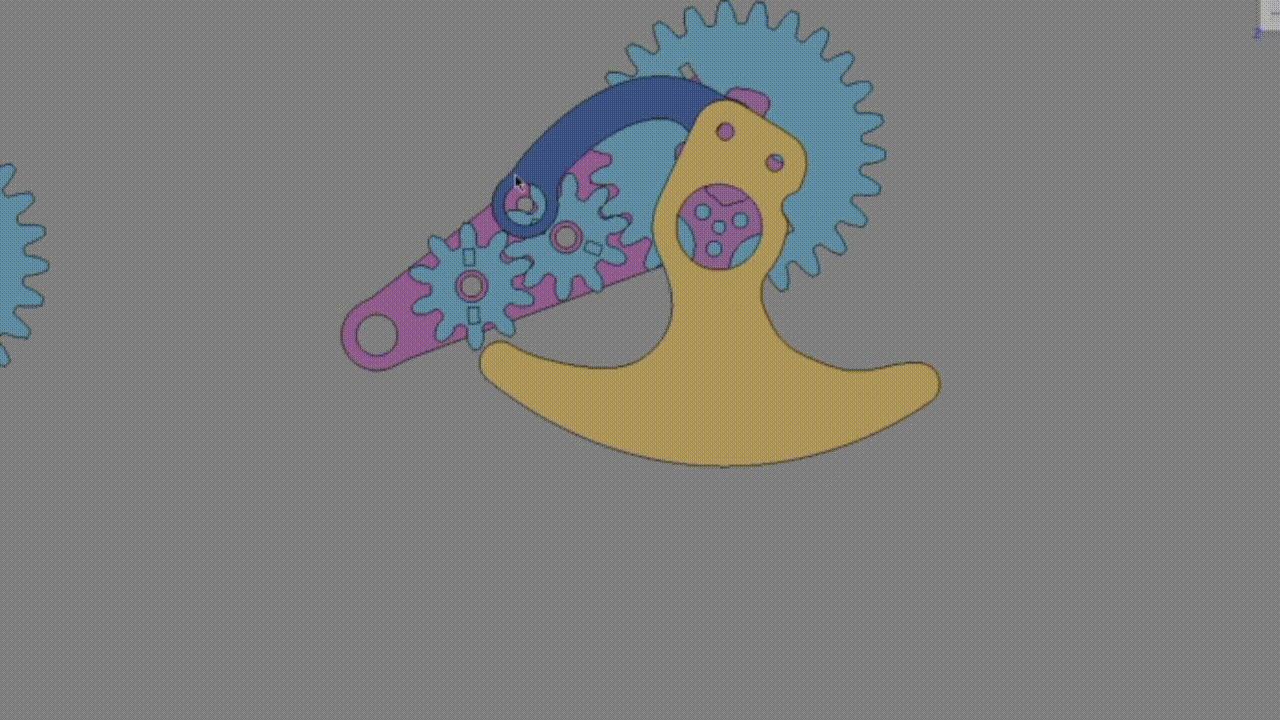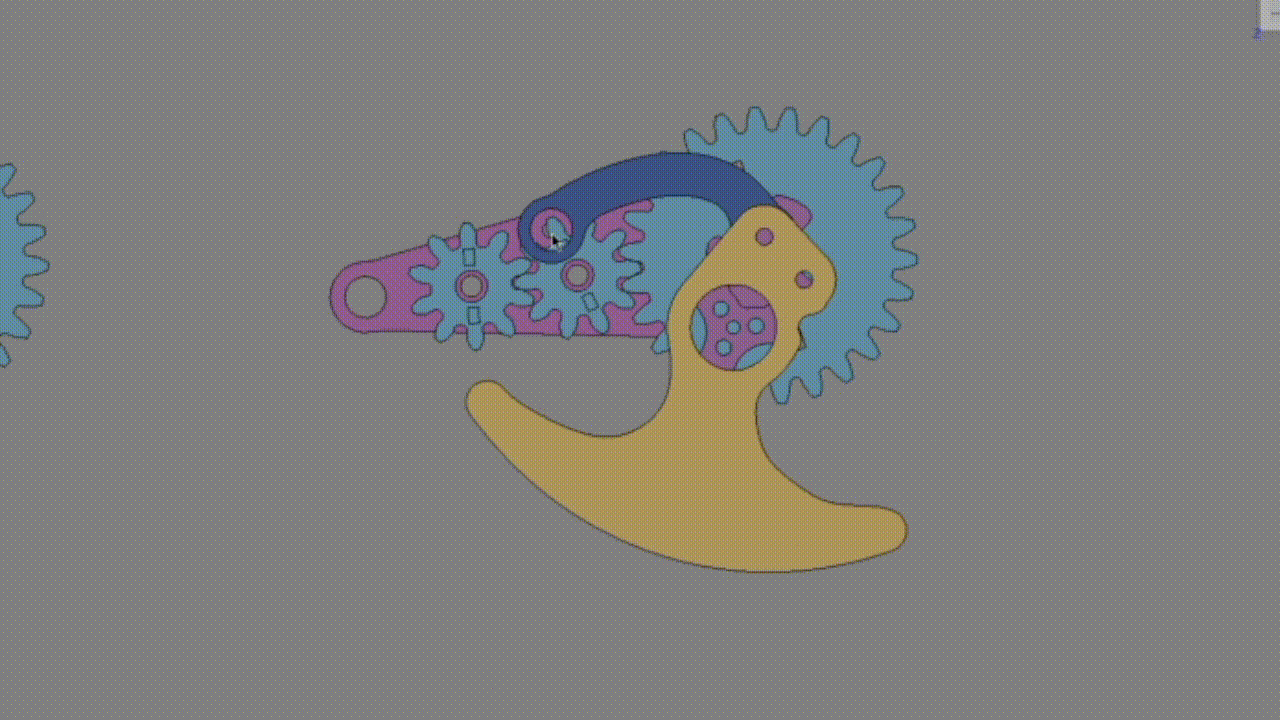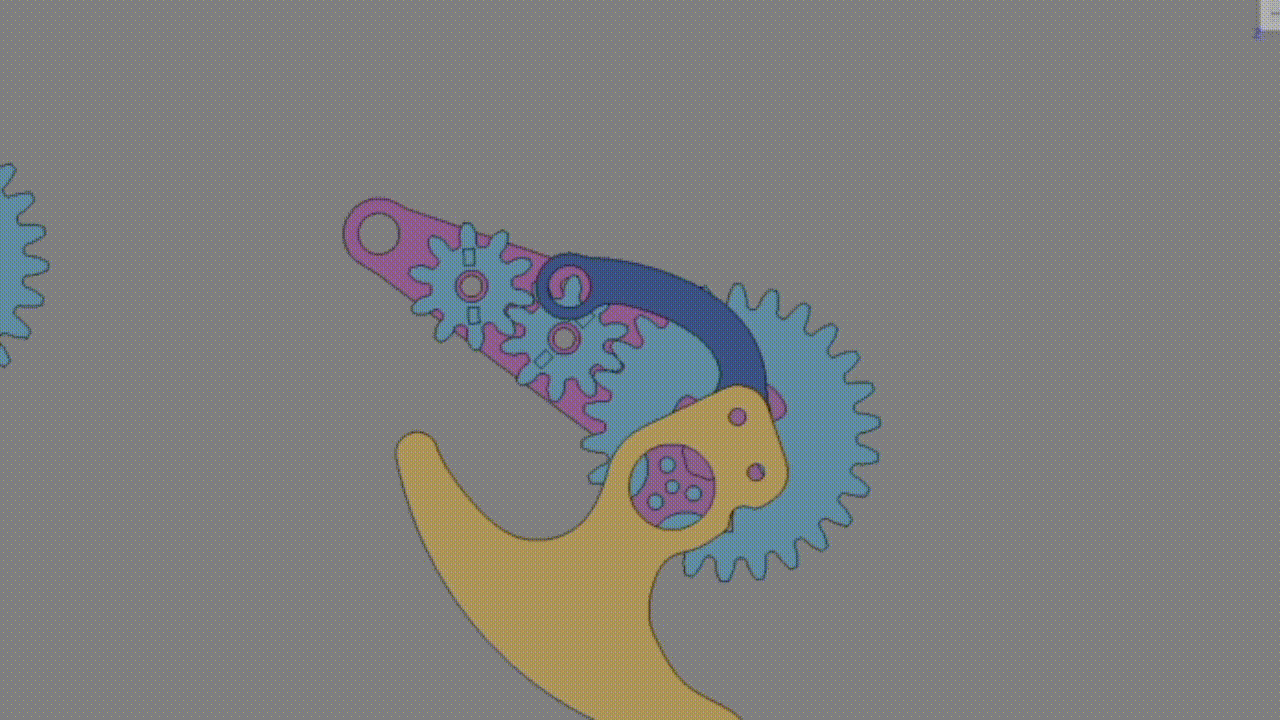2025/12/24 揺動させたゴイル脚について
立命杯に向けてゴイル脚を試作、実践投入した。その結果と設計についてつらつら書いていく
アームは既存の回転シールド、脚ユニットが今回試作したゴイル脚。
さっさと形にして試運転したかったため、3DPで試作。
 これが令和最新版ゴイル機体
これが令和最新版ゴイル機体
試運転動画~ツイッタより
1.概要
今回は以下コンセプトを満たせるような設計を目指した
・なるべく薄く作る →減速ギアを原動節にして最小構成
・走破性を上げる工夫 →脚先をスライダリンクにして「なるべく」揺動させる。
常に地面に対して平行な位置になっているより、角度をつけたほうがタイヤに近づくから特に段差とかには有利なんでないかと思ったのがきっかけ。

薄さに関しては脚ユニットの幅(側板の外側同士)33mm。
ヘッケン脚ユニットの幅は57mmなので、当社比ではかなり薄くできていると思う。

回転シールドに乗せたところ、機体幅270mmになりシールドの幅に余地ができすぎた。
横幅300mmの回転シールドも夢じゃない。小型機を丸呑みできるぞ!!
2.実戦投入してみて
と、いうのも1戦(ほぼ2分の激戦)で動作不能になり、その後フィールドを走ることはなかった。
試合中の動作感としては 震える!鳴る!滑る! で
揺動させるとかそういうレベルの話ではなく、 「超振動」をどうにか対策しないといけない。
平地で試運転させた時はそこまでスリップ感はなかったが、実際のフィールドだと段差で滑りまくっていた。
サスペンション機構は伝達ギアの軸から回転させて、緩い輪ゴムで引っ張っていただけなので、逆に推力が逃げてしまっていたみたい。
破壊箇所は以下
 脚ユニットが押されて歪んだ拍子に自分の回転シールドで殴って割れたとされる。破片をまき散らしてもうた
脚ユニットが押されて歪んだ拍子に自分の回転シールドで殴って割れたとされる。破片をまき散らしてもうた
 ギア欠け。これは単に組付けが悪く、嚙み合わせる位置が歯幅の端っこすぎた。
ギア欠け。これは単に組付けが悪く、嚙み合わせる位置が歯幅の端っこすぎた。
あとは脚のリンクが反転したりして、ロックした状態で無理やり動かそうとしたのもよくなかった。
3.設計、内部構造
設計10月 印刷、組み立て11月〜立命館前日
切削だったら組み立てまで間に合って無かったと思う。作り直しを何回もしている時は3DPの恩恵を一番感じた。プリンタはbambu A1
先端が地面をほぼ平行を向く系のブレードとリンクは同じで、原動節と長さの違う従動節を回転中心をずらして配置して、スライダ脚でつなぐ。


原動節、従動節、揺動節、固定節からなる。揺動節は各ユニット10個。1相。
素材はamazonのPETG脚先はシリコンシートを細かく切って貼っている。
プリントした脚に付きにくいのと設置面積も小さいからめっちゃ剥がれる。
従動節を外すとこのような内部構造になる外側が揺動する脚先で、内側は平行リンクになっており、原動節から揺動節へ回転を伝達している。
摺動部分は全てベアリング!!
アリエクで計5000円くらい。はずれなしだった (6803ZZ x10pcs,MR95ZZ x60pcs,MR85zz x60pcs)
原動節にはφ5のアルミ軸に内径5外径8のベアリングを入れ、M3皿ネジ(頭φ6)で上からしめて抜け止めにしている。PETGに直接ネジを切っている。
 これは完全自己流だが、PETGはφ2.7くらいの穴にネジを押し付けて無理やり締めることで緩みにくいタップが切れる。粘っこさのせいでネジが食いついて全然弛まない。
これは完全自己流だが、PETGはφ2.7くらいの穴にネジを押し付けて無理やり締めることで緩みにくいタップが切れる。粘っこさのせいでネジが食いついて全然弛まない。
このパイン飴みたいなのが5年ものの自作セットカラーで繰り返し開け閉めしても耐えている。
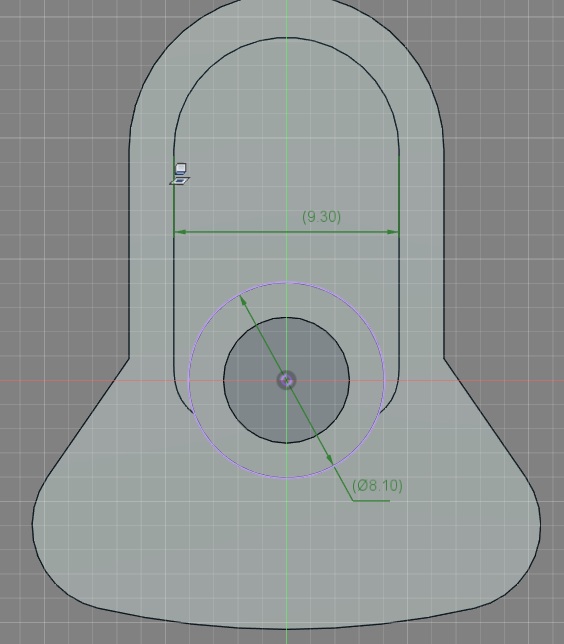
スライダ脚は原動節のベアリングが通る穴はφ8 スライダのベアリングはφ9にすることで反転防止のストッパを設けた。
片面から切削でつくれるようになっている。
従動節は3dプリンタで軸まで生やし、ベアリング入れてから先端をかしめて抜けないようにしている。
このパラメータは切り替えしをギリギリまで攻めている。原動節と揺動節が一番近い時で2.4mm これを2.0mmで作った時はリンクがすぐ反転して脚先が1回転してしまった。
修正後でも動かしている間に反転することがたまにあったので、攻めすぎは禁物。各パーツの剛性も重要になってくる。
4.まとめ
脚幅が薄くできるというのはメリットだが、現代のバトルスピードについていくにはまだまだ改良が必要。
リンク構造、サスペンション、足裏等々
4脚ともゴイルにせずとも後脚はヘッケンでもいいのでまたリベンジしたい
2025/9/17 遊星歯車の計算方法から考える、最適なサスペンション設計
昨今のかわロボでは標準搭載となったサスペンション。そのほとんどがギアトレインがサスペンションのリンクの一部になっており、満足いく性能にするにはは試行錯誤が必要になるだろう。
今回は、サスペンションのギアトレイン歯数や枚数(奇数or偶数)に着目し、動作の違いを紹介する。
1. 概要
かわろぼに用いられる脚のサスペンションのギア構造は遊星歯車の遊星歯車とキャリアの関係に置き換えることができ、後述の遊星歯車の速度比の計算式を流用して計算できる。
まず、理想のサスペンションの性能は以下のように定義する
「サスが稼働したときに脚機構が回転しないこと」
障害物に追従させるためのものなので、脚の回転と連動してしまうと効きにくくなってしまう。
遊星歯車で言うと、キャリアが動いても遊星歯車が回らないこと。
これを満たすギア設計は以下のようになる
| サスペンション方式 |
奇数枚 or 偶数枚 |
歯数の関係 |
| 平行リンク |
奇数枚 |
回転中心歯車の歯数 = 出力歯車の歯数 |
| 回転サス |
奇数枚 |
回転中心歯車の歯数 << 出力歯車の歯数 |

※リンク外のギアは計算結果に影響しない(脚の回転方向には影響する)
以下より計算例を紹介していく
2. 遊星歯車機構について
遊星歯車機構は、太陽歯車・遊星歯車・内歯車・キャリアから構成され、固定する歯車により3種類ある
- プラネタリ型: 内歯車を固定
- ソーラ型:太陽歯車を固定
- スター型: 遊星キャリアを固定
今回の計算では太陽歯車を固定するソーラ型の速度比計算方法を使用する。
固定:太陽歯車
入力:内歯車
出力:キャリア
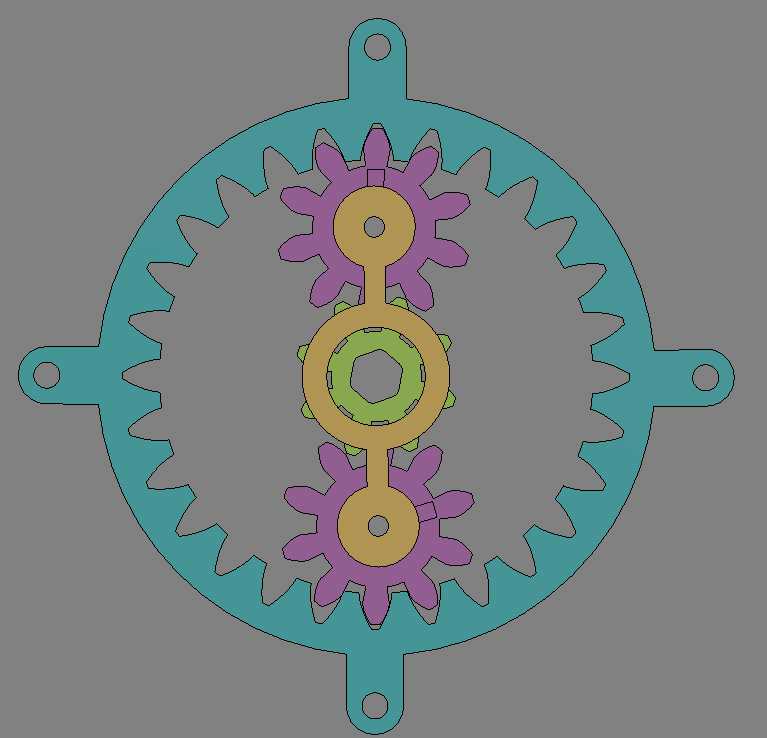
3. 遊星歯車機構速度比の計算
糊付け法という手法で計算を行う。
① キャリアを固定して太陽歯車を1回転させ、その時の他の歯車の回転数を計算する。
② 太陽歯車が回転した分を逆回転させる(歯車全部を糊付けして回転)。
③ ①+②の値を入力歯車/出力歯車として速度比を求める。
参考:https://www.khkgears.co.jp/gear_technology/intermediate_guide/KHK388.html
太陽歯車の歯数=Za、遊星歯車=Zb、内歯車=Zc
ソーラ型の速度比計算
| 回転数 |
太陽歯車 Za |
遊星歯車 Zb |
内歯車 Zc |
キャリア |
| ① |
1 |
-Za/Zb |
-Za/Zc |
0 (固定) |
| ② |
-1 |
-1 |
-1 |
-1 |
| ①+② |
0 (固定) |
-Za/Zb-1 |
-Za/Zc-1 |
-1 |
内歯車Zc/遊星キャリアの速度比は、(-Za/Zc-1)/-1 となる。
4. かわロボの脚に置き換えた計算
かわロボの脚の場合は内歯車をヘッケンクランクに固定接続される出力歯車に置き換えて、
キャリア/出力歯車を計算する。内歯車→平歯車に置き換わることで、Zcの回転方向は遊星歯車の計算と反対になる。
また、実際のギトレインでは回転中心から出力歯車まで複数枚で構成されているが、
遊星歯車の枚数が奇数が偶数で速度比が大きく変わる。
計算方法
① キャリアを固定して太陽歯車を1回転させ、他の歯車の回転数を計算する。
② 太陽歯車が回転した分を逆回転させる(歯車全部を糊付けして回転)。
③ ①+②の値をキャリア/出力歯車として減速比を求める。
・奇数枚の場合 (歯数が太陽歯車 ≒ 出力歯車)

| 回転数 |
太陽歯車 Za |
遊星歯車 Zb |
出力歯車 Zc |
キャリア |
| ① |
1 |
-Za/Zb |
Za/Zc |
0 (固定) |
| ② |
-1 |
-1 |
-1 |
-1 |
| ①+② |
0 |
-Za/Zb-1 |
Za/Zc-1 |
-1 |
⇒減速比=出力歯車Zc(①+②)/キャリア(①+②)=1-Za/Zc
Zc=20、Za=10 とするとキャリアを1回転させると出力歯車が0.5回転する。
歯数が太陽歯車=出力歯車の場合はZa=Zcとなり、減速比=0。キャリアが動いても出力歯車が動かない。
・偶数枚の場合 (歯数が太陽歯車 ≒ 出力歯車)

| 回転数 |
太陽歯車 Za |
遊星歯車 Zb |
遊星歯車 Zb2 |
出力歯車 Zc |
キャリア |
| ① |
1 |
-Za/Zb1 |
Za/Zb2 |
-Za/Zc |
0 (固定) |
| ② |
-1 |
-1 |
-1 |
-1 |
-1 |
| ①+② |
0 |
-Za/Zb1-1 |
Za/Zb2-1 |
-Za/Zc-1 |
-1 |
⇒減速比=Zc(①+②)/キャリア(①+②)=1+Za/Zc。
歯数が太陽歯車=出力歯車の場合はZa=Zcとなり、減速比2。
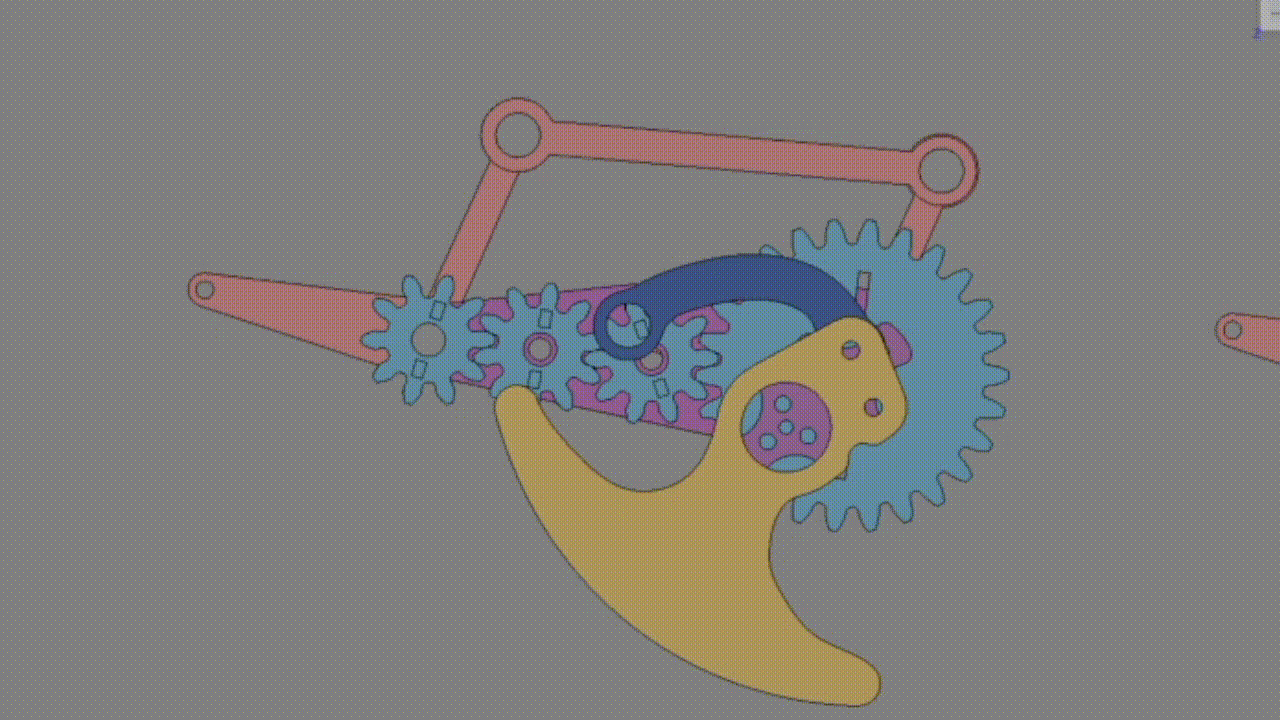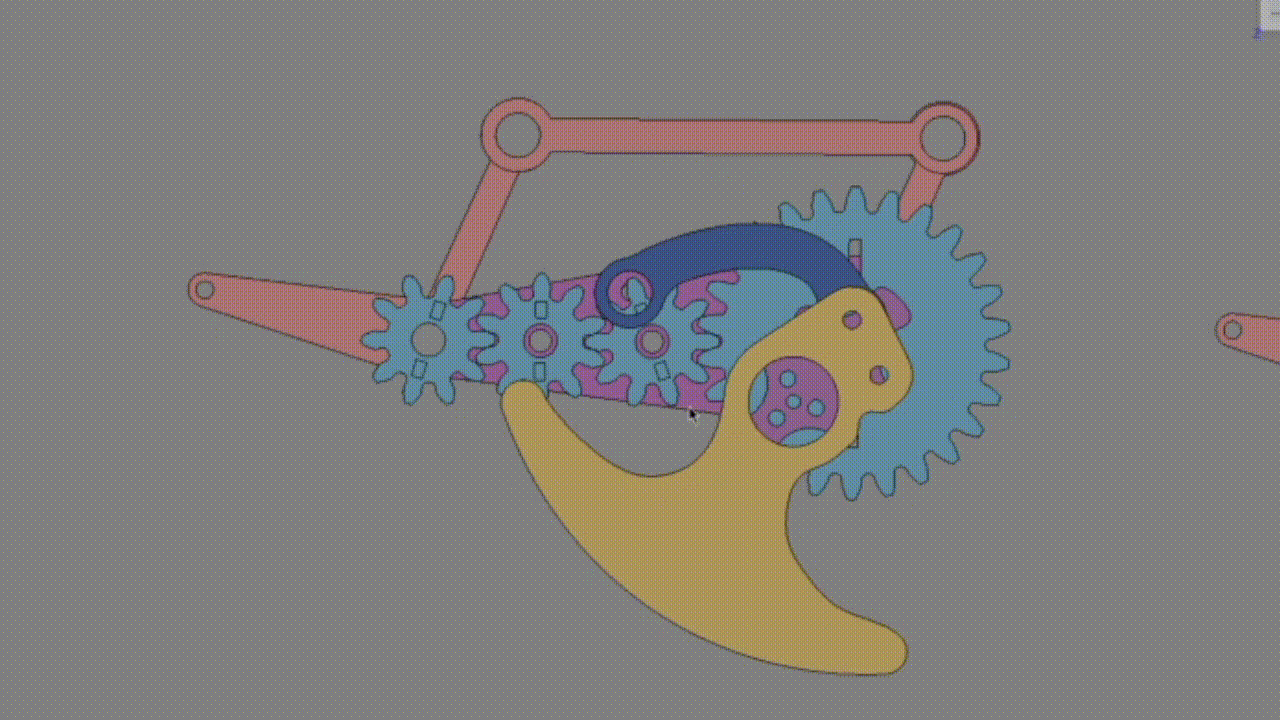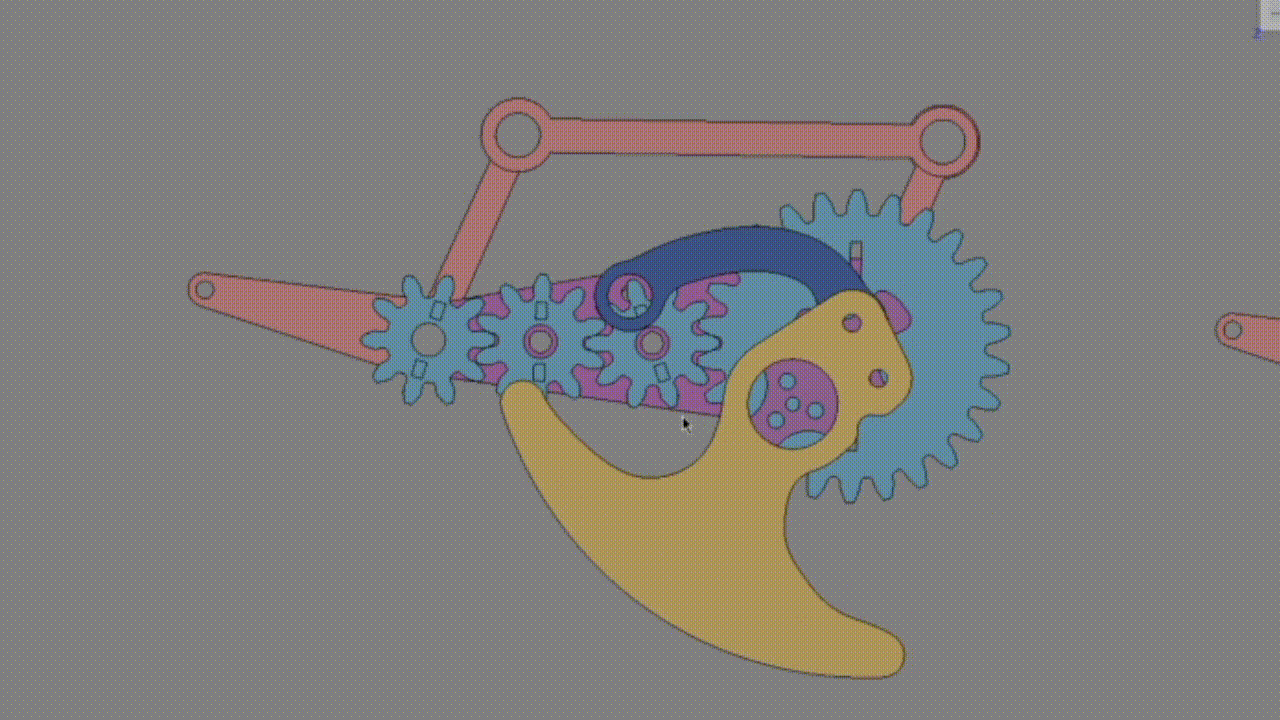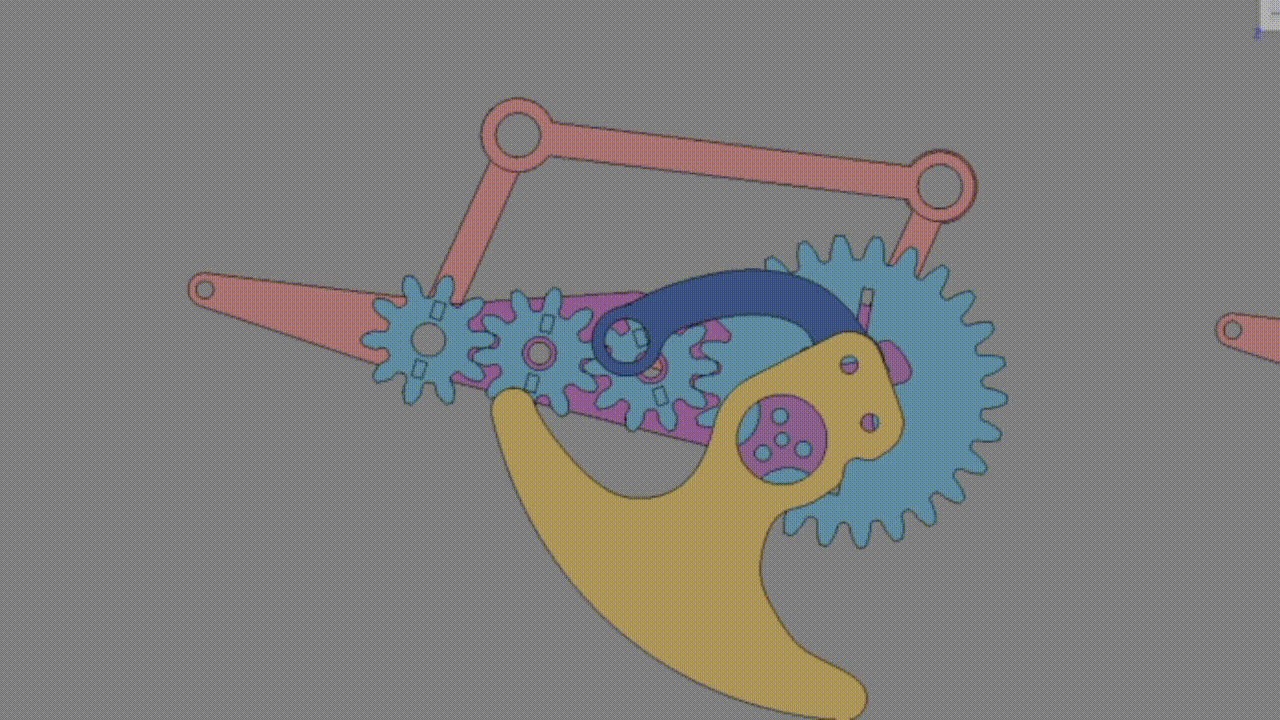
5. 平行リンクの計算
キャリアに対して出力ギアが動くほど脚が回転するため、キャリアと出力歯車の速度比を0にすることが最適である。偶数枚だと必ず1以上の速度比になることから奇数枚にする必要がある。
出力歯車Zc/キャリア = 1-Za/Zc=0 となるようにする。 Za=Zcが理想。
出力歯車の歯数を回転中心の歯車に近づけるほど回転数が小さくなる。

6. 回転サスの計算
平行リンクとの違いは、脚のヘッケン軸がキャリアと接続されているという点である。この場合、脚のリンクがキャリアとともに動く。キャリアと出力歯車の速度比を同じにする(1に近づける)ことでサスが効きやすくなる。
出力歯車Zc=1-Za/Zc=1 となるようにする。 Za<Zcとするほど回転数が1に近づく。
奇数枚、偶数枚では脚の回転方向が反対になる。
奇数の場合:
1-Za/Zcより必ずキャリアより出力歯車が少なく回る → 脚がキャリアの動きと逆に動く。
サスが上に上がる → 脚が前進方向に進む。
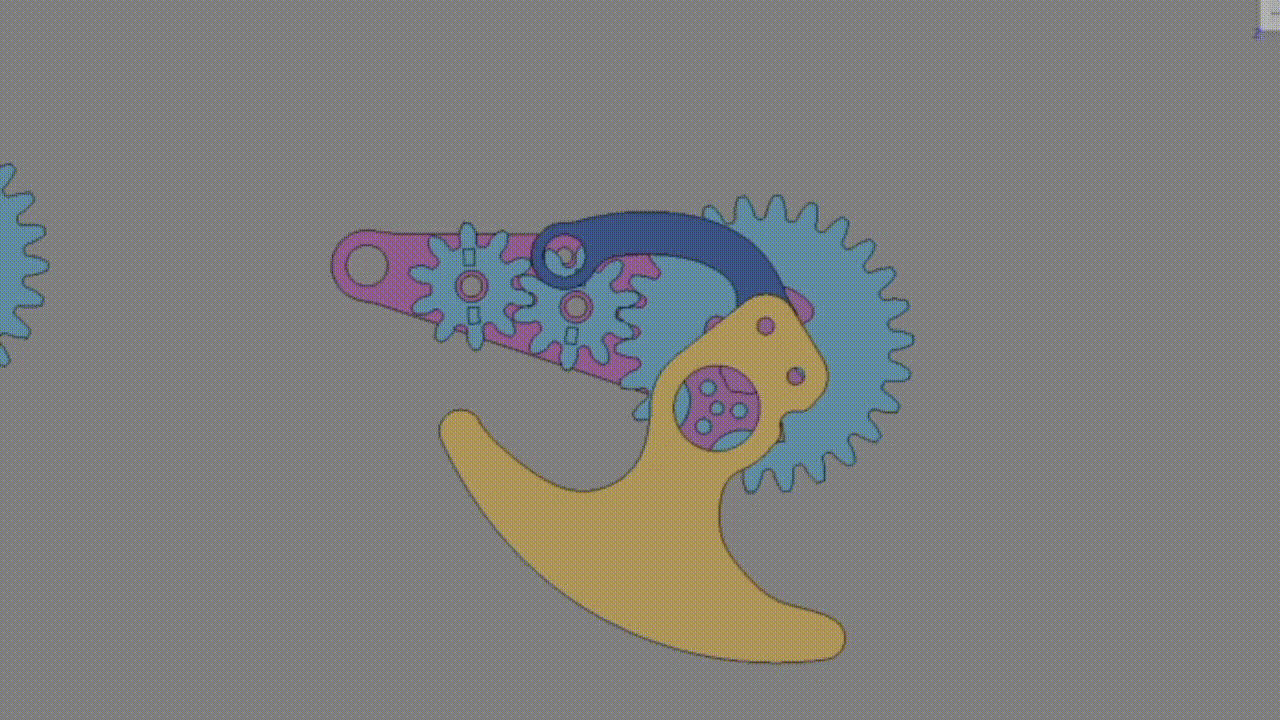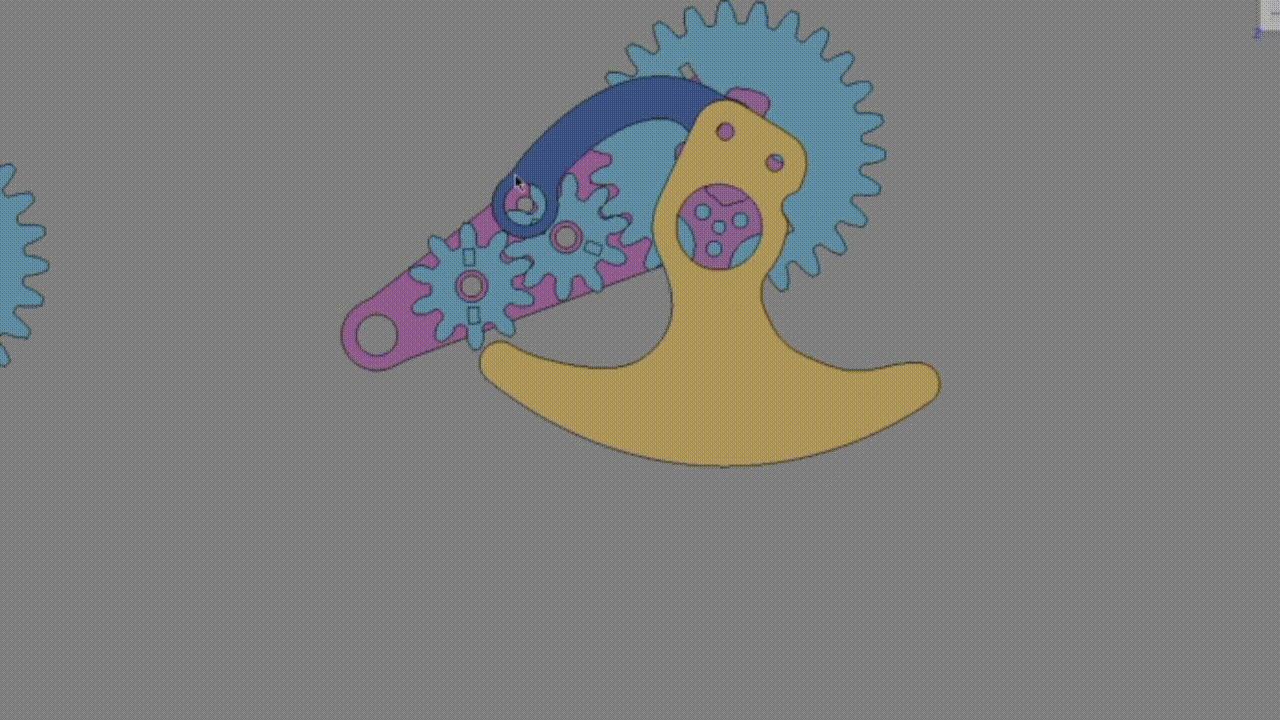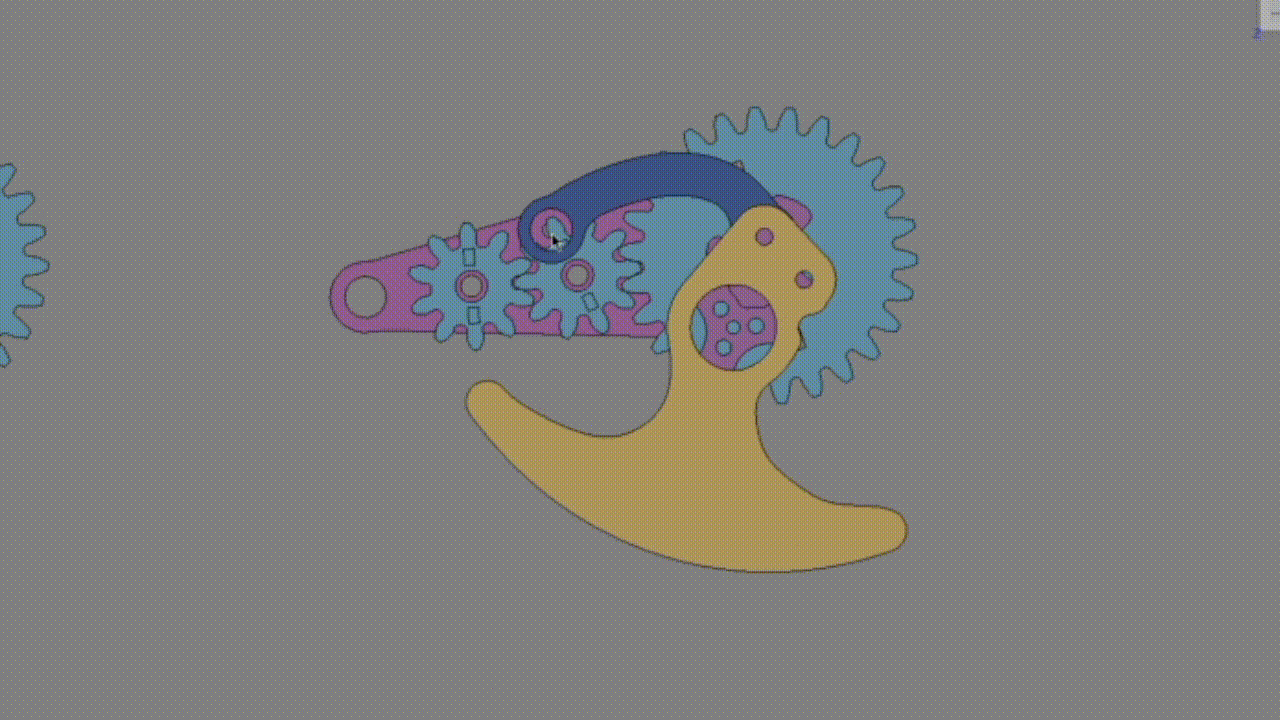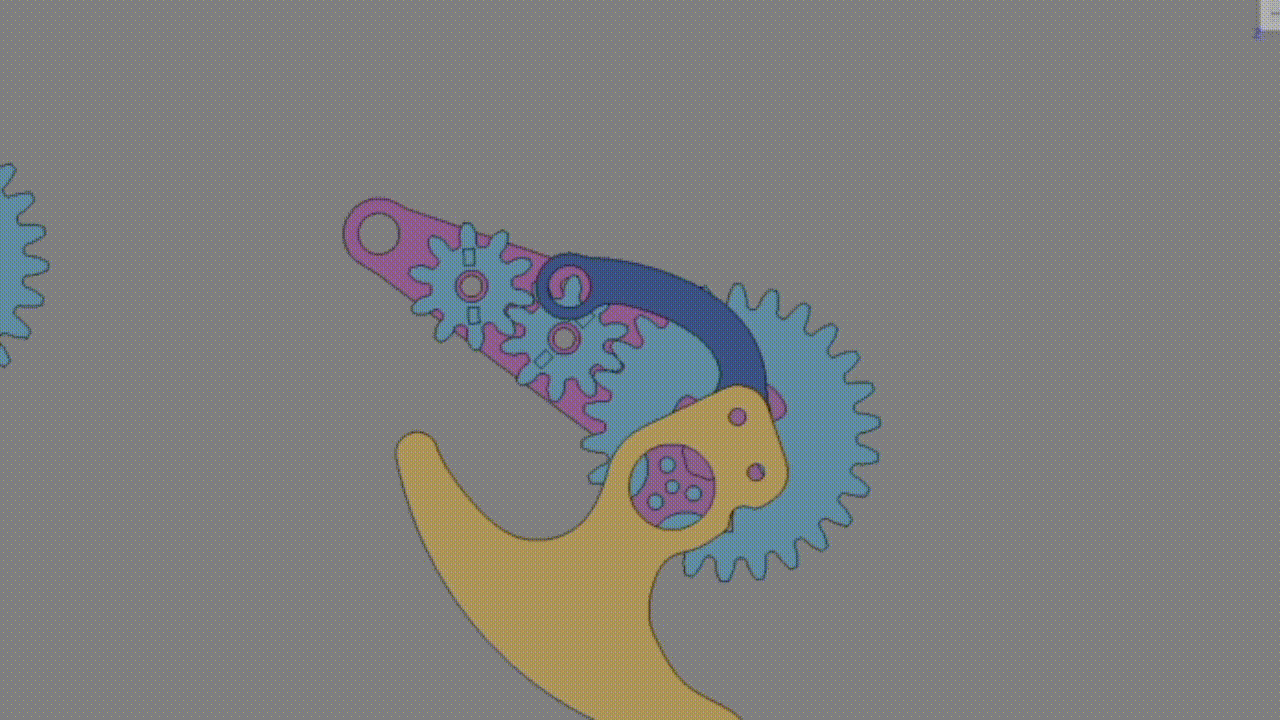

偶数の場合:
1+Za/Zcより必ずキャリアより出力歯車が多く回る → 脚がキャリアの動きと同じ方向に動く。
サスが上がる → 脚が後進方向に進む。
偶数枚では後進方向に進んでしまうため、奇数枚にする。※これに関しては諸説あるかもしれない
以下、サスが稼働したときに脚機構が回転しない条件
| サスペンション方式 |
計算式 |
奇数枚の時 |
偶数枚の時 |
| 平行リンク |
キャリア(①+②)/出力歯車Zc=0 |
1-Za/Zc=0 |
1+Za/Zc=0 |
| 回転サス |
キャリア(①+②)/出力歯車Zc=1 |
1-Za/Zc=1 |
1+Za/Zc=1 |
これが令和最新版ゴイル機体
脚ユニットが押されて歪んだ拍子に自分の回転シールドで殴って割れたとされる。破片をまき散らしてもうた
ギア欠け。これは単に組付けが悪く、嚙み合わせる位置が歯幅の端っこすぎた。
これは完全自己流だが、PETGはφ2.7くらいの穴にネジを押し付けて無理やり締めることで緩みにくいタップが切れる。粘っこさのせいでネジが食いついて全然弛まない。